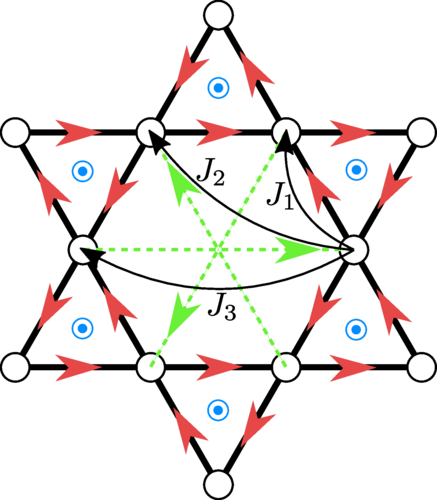
Recently we published in Phys. Rev. B our new work, where we use a mean field treatment to study the phase diagram of the Heisenberg model on the Kagome lattice. Motivated by recent works on the effective description of TMD heterostructures by Heisenberg-like interactions, we develop a Schwinger boson mean field theory to study the phase diagram of the $J_1-J_2-J_3$ Heisenberg model with Dzyaloshinskii-Moriya interactions. We opted for this method since it is particularly useful to distinguishing long range magnetic orders and gapped spin liquid phases, an exotic phase of matter in which the spin motion continues down to zero temperature. In this work we extend our search also to chiral solutions of the mean field equations and perform an extensive projective symmetry group classification of the possible phases. We find that gapped chiral spin liquid solutions appear as ground states in possibly material-relevant regions of the phase diagram and we find a new solution which was never observed as stable in such Schwinger boson treatments.