Aller au contenu directement

Research

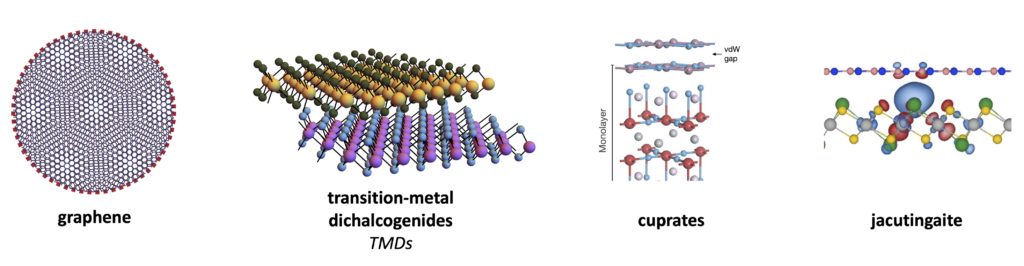
We are interested in new flat materials that are correlated and highly tunable (using stacking, twist angles and gates). This tunability opens up the possibility to resolve some long-standing ‘strange’ condensed matter problems, such as the nature of doped Mott insulators and electronic interaction driven superconductivity.

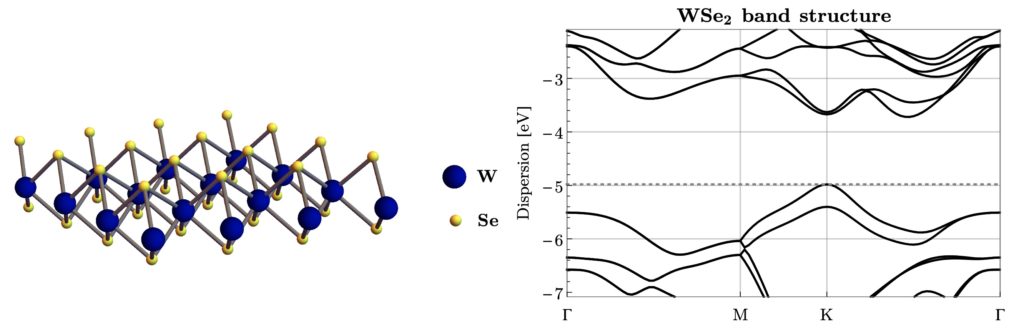
We theoretically study materials where heterostructure engineering enhances interaction effects (moiré materials), and the monolayer limit of correlated materials (pnictides, cuprates and organics).

What is “strange” matter?

In most materials, electronic interactions play a minor role, and one can treat the system as effectively noninteracting, with electron bands described by density functional theory. The main effect of interactions is to spontaneously break a symmetry, which explains the existence of crystals, magnets, superconductors, and so forth. The combination of band theory and symmetry breaking is immensely powerful, and lies at the heart of the enormous success of condensed matter theory and experiments.

Electron bands are a good description of most weakly interacting materials, such as monolayer WSe2. This band structure is calculated using density functional theory.

Further readings

  • An Introduction to Spontaneous Symmetry Breaking, Aron J. Beekman, Louk Rademaker, Jasper van Wezel, SciPost Phys. Lect. Notes 11 (2019); arXiv:1909.01820.
  • A Practical Introduction to Density Functional Theory, Louk Rademaker, (2020), arXiv:2011.09888 .

Any material whose properties cannot be described by band theory and symmetry breaking is strange. This includes the strange metal phase observed in cuprates, twisted bilayer graphene, and moiré TMDs, where the resistivity is linear in temperature in defiance of Fermi liquid theory. Other strange electronic phases include the (doped) Mott insulator, superconductors with unconventional pairing mechanisms, and highly entangled topological phases such as spin liquids.

The appearance of replica bands is a signature of the forward scattering mechanism of superconductivity.

Further readings

  • How to recognize the universal aspects of Mott criticality? Yuting Tan, Vladimir Dobrosavljević, Louk Rademaker, Crystals 12, 932 (2022); arXiv:2206.02055.
  • Enhanced superconductivity due to forward scattering in FeSe thin films on SrTiO3 substrates, Louk Rademaker, Yan Wang, Tom Berlijn and Steve Johnston, New J. Phys. 18, 022001 (2016); arXiv:1507.03967.

In addition to strongly correlated and topological matter, we also study interacting disordered matter. This can lead to the emergence of many-body localization and electron glassy behavior. The strangeness is here manifest due to the breakdown of thermodynamics.

Geometrical frustration in triangular organics leads to the formation of an electron glass with inhomogeneous charge order.

Further readings

  • Scaling theory of few-particle delocalization, Louk Rademaker, Phys Rev. B 104, 214204 (2021); arXiv:2107.06364.
  • Glassy dynamics in geometrically frustrated Coulomb liquids without disorder, Samiyeh Mahmoudian, Louk Rademaker, Arnaud Ralko, Simone Fratini and Vladimir Dobrosavljevic, Phys. Rev. Lett. 115, 025701 (2015); arXiv:1412.4441.
The two-dimensional Hubbard model is a simple yet unsolved model that contains Mott physics and unconventional superconductivity.

Why “flat” matter?

Matter in two dimensions – that is: flat – has some unique properties that make it more likely to be strange.

In higher dimensions than two, symmetry broken states are almost unavoidable. In fact, above the upper critical dimension, the properties of many materials can be exactly described by mean field theory. While physics in one dimension does realize its own set of “strange” physics (for example Luttinger liquids), many 1d models are exactly solvable (through Bethe ansatz, bosonization). For those interested in one-dimensional physics, we do have an excellent research group headed by Thierry Giamarchi.

In contrast, many phenomena are special in 2d: the Kosterlitz-Thouless transition (only happens in 2d); Anderson transition (critical in 2d); the breakdown of Hertz-Millis quantum phase transition theory in 2d; Mermin-Wagner theorem that prohibits the existence of two-dimensional materials; the (fractional) Quantum Hall effect; the existence of anyons; and so forth.

Flat Club seminars

In Geneva we organize biweekly Flat Club meetings, where we discuss the latest exciting results in the field of flat quantum matter physics. Please register at the Flat Club website if you are interested in joining our meetings.

More about Flat Club